1. Introduction
용수철에 대한 식은 우리 모두가 잘 알고 있다. F=-kx, (F는 힘, k는 용수철 상수) -k를 비례상수로 하는 상수항이 없는 x에 대한 일차식이 그것이다.
이와 비슷하게, 비틀림 진자에서도 τ=κθ(τ는 토크, κ는 비틀림 용수철 상수, θ는 각변위)의 θ에 대한 상수항이 없는 일차식 관계가 나타난다.
이를 이용하여서 1) 비틀림 용수철 상수 κ를 구하고, 2) 속이 빈 원통의 관성 모멘트를 구하고 3) 두 개의 비틀림 용수철 상수를 병렬로 연결하였을 때의 합성 비틀림 용수철 상수를 구하고, 이론적인 근거를 찾아보는 것이 목적이다. 덧붙여, 만일 직렬로 연결하면 어떻게 될지에 대해서도 추론하여 보았다.
2. 기본 이론
복원력에 대한 Hooke의 법칙은 F=kx(k: 용수철 상수) 꼴로 주어진다. 이와 비슷하게 비틀림 스프링에서도 복원 토크에 대한 식이 성립한다. τ=κθ(κ역시 와이어의 물성에 의존하며, 비틀림 스프링 상수라 부른다.)
그리고 SHO에서의 주기가 T=2π sqrt(m/k)이었듯이, 비틀림 진자에 의한 SHO는 T=2π sqrt(I/κ)로 주어진다. 디스크의 관성 모멘트는 1/2 MR^2이다.
디스크가 여러 개 있는 경우에는 마치 총 질량을 구할 때 M=ΣMn
이라고 구했듯이, 축이 같은 여러 물체의 총 관성모멘트는 I=ΣIn로 구할 수 있다.
3. 실험 결과
장비 설치 및 실험
우선 장치에 사용될 재료들의 무게를 측정하였다.
 |
 |
 |
 |
 |
운이 좋게도 양 옆 추의 무게가 같게 나왔다. |
각 축바퀴의 지름과 길이 등도 측정하였다.
 |
 |
 |
 |
 |
 |
 |
막대의 길이는 0.38m 추의 길이가 2cm 이므로 추를 점질량으로 가정하였을 때 중심으로부터의 거리는 각각 0.18m 이다. |
이로부터 관성 모멘트들을 이론적으로 계산하여 보자.
| 물체 | 관성모멘트(kg∙m2 ) |
| 막대 | 3.3693×10-4 |
| 추 | 2.4462×10-3 |
| 막대 + 추 | 5.2293×10-3 |
| 알루미늄 디스크 | 1.3623×10-4 |
| 속이 빈 검은 링 | 5.2580×10-4 |
| 받침대 + 검은 링 | 6.6203×10-4 |
단, 추는 회전축으로부터 0.18m 떨어진 곳에 있는 점질량으로 취급하였다. 추는 2개이다. 막대와 추의 관성모멘트, 받침대와 검은 링의 관성모멘트는 회전축이 같으므로 단순 합산이 가능하다.
이제 실험을 진행하였다.
실험 1) 비틀림 스프링 상수 측정
세 가지의 와이어가 있었다. 굵은 와이어, 중간 와이어, 얇은 와이어|
이 세가지 와이어에 대한 스프링 상수를 각각 측정하였다.
 |
 |
 |
결과는 이와 같이 나왔다.
| 용수철 종류 | 비틀림 용수철 상수 κ |
| 얇은 와이어 | 0.0129 |
| 중간 와이어 | 0.0389 |
| 굵은 와이어 | 0.11 |
실험 2) 관성 모멘트 측정
실험 2부터는 중간 두께 와이어와 두꺼운 와이어만 사용하였다.
첫번째로 알루미늄 디스크와 검은 링의 관성모멘트 측정을 위해서 각속도 ω를 측정하였다.
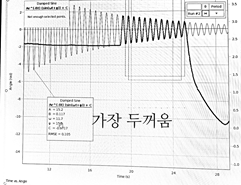 |
 |
| 와이어(막대) 종류 | 진동수(rad/s ) | 진동 주기(s) 실험치 | 진동주기(s) 이론치 |
주기오차 (%) |
비틀림 용수철 상수 |
| 굵은 와이어(막대) | 11.7 | 0.537 | 0.487 | 9.31 | 0.11 |
| 중간 와이어(막대) | 7.12 | 0.882 | 0.819 | 7.14 | 0.0389 |
이를 통해 구한 디스크와 검은 링의 합성 관성 모멘트 I는 I=κ/ω^2 에 의해 다음과 같이 나온다.
| 와이어(막대) 종류 | 관성모멘트 실험치(kg∙m2 ) | 이론치와의 오차(%) |
| 굵은 와이어(막대) | 8.0356×10-4 | 17.61 |
| 중간 와이어(막대) | 7.6734×10-4 | 13.72 |
관성 모멘트의 이론치: 6.6203×10^(-4)kg∙m^2
두 번째로 막대와 양 끝에 달린 추의 합성 관성 모멘트 측정을 위해서 각속도 ω를 측정하였다.
 |
 |
| 와이어(막대) 종류 | 진동수(rad/s ) | 진동 주기(s) | 진동주기(s) 이론치 |
주기오차 (%) |
비틀림 용수철 상수 |
| 굵은 와이어(막대) | 4.32 | 1.454 | 1.369 | 5.85 | 0.11 |
| 중간 와이어(막대) | 2.60 | 2.416 | 2.302 | 4.72 | 0.0389 |
이를 통해 구한 막대와 추의 합성 관성 모멘트 I는 I=κ/ω^2 에 의해 다음과 같이 나온다.
| 와이어(막대) 종류 | 관성모멘트 실험치(kg∙m2 ) | 이론치와의 오차(%) |
| 굵은 와이어(막대) | 5.8942×10-3 | 10.128 |
| 중간 와이어(막대) | 5.7544×10-3 | 9.125 |
관성 모멘트의 이론치: 5.2293×10^(-3)kg∙m^2
실험 4 비틀림 용수철 두 개를 합친 경우

와이어 두 개를 겹친 경우에 비틀림 용수철 상수가 어떻게 될까에 대한 이론적 예측을 해 보았다. 와이어 두 개를 병렬 연결한 것은 τ=κθ에서 각각의 용수철에 같은 크기의 변형이 발생하는 상황이다.
그러므로 비틀림 각도는 크기가 같다. 각각의 용수철에 작용하는 토크 τ는 τ1=κ1θ, τ2=κ2θ이고 총 토크 τ=τ1+τ2=κ1θ+κ2θ=κ_Total θ
따라서 병렬 연결의 경우,
κ1+κ2=κ_Total
일 것으로 예상하였다. ω=6.76rad/s이므로 T=2π/ω의 관계를 이용하면 κ=I(2π)^2/T^2=Iω^2=0.1270가 나온다.
| 용수철 종류 | 비틀림 용수철 상수 κ |
| 얇은 와이어 | 0.0129 |
| 중간 와이어 | 0.0389 |
| 굵은 와이어 | 0.11 |
앞서 측정한 굵은 와이어와 중간 와이어의 비틀림 용수철 상수의 합은 0.11+0.0389=0.1489로, 이론상 값과의 오차는 대략 (0.1489-0.1270)/0.1489×100%=14.70% 정도가 났다.
3. 직렬 연결을 하였을 때의 결과 추론
와이어 두 개를 직렬 연결한 것은 각각의 각변위의 크기의 합성이 총 각변위가 되는 상황이다. τ=κθ에서 각각의 용수철에 같은 크기의 토크가 가해지고 있다.
θ=θ1+θ2=τκ1+τκ2=τκ_Total 이 성립한다.
따라서 두 용수철을 직렬 연결할 경우에는1/κ1+1/κ2=1/κ Total의 관계를 만족할 것으로 예상한다.
4. 오차의 원인 분석
1) 축(도르래) 바퀴의 관성모멘트를 고려하지 않음
2) 와이어를 고정하는 막대의 관성모멘트를 고려하지 않음
3) 와이어 고정하는 막대의 경우에 기계 내부의 기어 때문에 마찰력이 존재하여 추가적으로 감쇠 효과를 냄
4) 알루미늄 디스크의 경우 완벽한 원판이 아니라 구멍이 존재하여 이것이 관성모멘트 크기에 영향을 미치는데 이를 고려하지 않음
5) 와이어가 많은 실험으로 인해서 휘어진 상태였음
5. 참고 문헌
한양대학교 역학실험실
고려대학교 교양물리실험실
Classical Dynamics for Particles and Systems(Thornton)
'Classical Mechanics > Experiments - Lynx' 카테고리의 다른 글
| 역학실험 6- 진폭이 큰 진자의 주기 - 2 (0) | 2021.07.25 |
|---|---|
| 역학실험 6 - 진폭이 큰 진자의 주기 - 1 (0) | 2021.07.19 |
| 역학실험 5 - 기울어진 진자의 운동 (0) | 2021.07.12 |
| 역학실험 4- 선운동량 보존/등가속도 운동 -(2) (0) | 2021.07.05 |
| 역학실험 4 - 선운동량 보존 & 등가속도 운동 -(1) (0) | 2021.06.28 |



