1. 실험 목적 및 소개
진동이 이루어지는 평면을 바꾸어, 진자에 가해지는 가속도의 크기를 바꿀 경우 진동주기가 어떻게 바뀌는지 탐구한다.
2. 기본이론
단진자의 주기는 우선 T=2π sqrt(L/a)이다. (a : 가속도, L : 점질량까지의 거리)
그러나 우리는 단진자가 아니라 물리 진자를 다루는 중이므로, 회전에 관련된 항을 추가로 도입하여야 한다. 따라서
T=2π sqrt(I/mar) ( I :축에 대한 계의 관성 모멘트, r :축에서 막대+ 추의 질량중심까지의 거리)가 성립함을 유도할 수 있다.
그런데 우리가 물리 진자보다는 단진자에 더 익숙하고 더 다루기 쉽다는 점 또한 분명하다. 그러므로 Effective length 라는 개념을 도입한다. 우리가 다루는 물리진자계를 이와 똑같이 행동하는 단진자로 바꾸어서 생각하는 것이다.
I,m,r을 보았을 때, 우선 I/mr은길이의 차원을 가지므로 L_eff=I/mr 라고 쓸 수 있다. (L_eff: Effective Length)
따라서 T=2π sqrt(L_eff/a)
로 고쳐 쓸 수 있다.
여기서 L_eff는 a=g(중력가속도) 인 경우에서 주기를 측정하여 결정하고자 한다.
L_eff=(T/2π)^2 g
그리고 우리의 실험에서는 가속도a가 g가 아닌 g의 cosine 성분만 유효하게 작용하는 상황에 대해서 주로 논할 것이다. (sine 성분은 막대에 작용하는 힘에 의하여 상쇄됨)

3. 실험
우선 막대, 추의 질량을 전자 저울을 이용해 측정하고, 길이도 측정하였다.

측정한 결과는 다음과 같다.
| 막대 전체 길이 | 0.35m | 막대 질량 | 0.02663kg |
| 추까지의 막대의 길이 | 0.16m | 추의 질량 | 0.08345kg |

막대의 끝에 추를 매달고, 처음에는 회전축을 막대의 왼쪽 끝부분으로, 나중에는 막대의 중간으로 두고 실험을 진행하였다.
다음은 실험 결과 데이터들이다.
< 1 > 회전축이 막대의 왼쪽 끝부분인 경우
| 각도(° ) | 각속도(rad/s ) |
| 0 | 5.59 |
| 5 | 5.58 |
| 10 | 5.57 |
| 15 | 5.51 |
| 20 | 5.43 |
| 25 | 5.30 |
| 30 | 5.19 |
| 35 | 5.07 |
| 40 | 4.90 |
| 45 | 4.68 |
| 50 | 4.51 |
| 55 | 4.17 |
| 60 | 3.79 |
| 65 | 3.50 |
| 70 | 3.12 |
| 75 | 2.63 |
| 80 | 2.09 |
| 85 | 1.34 |
측정한 후에는 다음과 같이 Damped sine 곡선 모양을 활용하여 각속도를 알아냈다.


데이터들을 정리하면 이렇게 나온다.
polyfitting 과정을 8차함수에 대해서 진행하면(m=8)
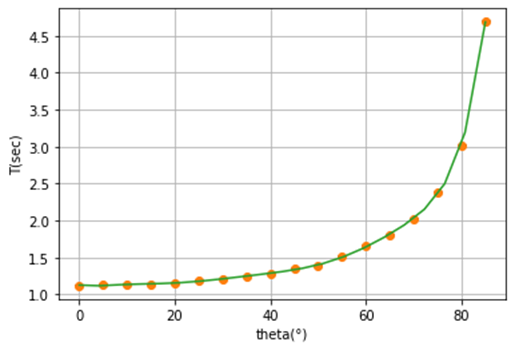
T=2π/ω를 이용하면 이러한 그래프를 얻을 수 있다.
< 2 > 회전축의 막대의 중심에 가까운 경우

| 각도(° ) | 각속도(rad/s ) |
| 0 | 7.31 |
| 10 | 7.19 |
| 20 | 7.00 |
| 30 | 6.81 |
| 40 | 6.38 |
| 50 | 5.73 |
| 60 | 5.08 |
| 70 | 4.15 |
| 80 | 2.71 |
이렇게 해서 그래프를 그려 보면

T=2π/ω
를 이용하면 이와 같은 그래프가 나온다. 그리고 마찬가지로 m=8일 때 polyfitting 과정을 거치면

의 그래프를 얻는다.
이로써, 예비 보고서에서 예측한 결과를 직접 확인할 수 있었다.
실험 결과를 이론과 비교한다.
Leff를 구하기 위해서 질량중심의 위치r, 관성 모멘트I, 총 질량M을 활용한다.
r=(m1x1+m2x2)/(m1+m2)
L_eff=I/mr=0.147m
< 1 >부터 살펴보자.
| 각도 | 주기(이론 sec) | 주기(실제 sec) | 오차(%) | ||
| 0 | 1.07668221 | 1.124 | -4.3952 | ||
| 5 | 1.07873662 | 1.12602 | -4.3831 | ||
| 10 | 1.0849552 | 1.12804 | -3.9712 | ||
| 15 | 1.09550823 | 1.14032 | -4.0909 | ||
| 20 | 1.11069451 | 1.15712 | -4.1803 | ||
| 25 | 1.13096634 | 1.18551 | -4.8225 | ||
| 30 | 1.15697032 | 1.21063 | -4.6382 | ||
| 35 | 1.18961183 | 1.23929 | -4.1757 | ||
| 40 | 1.23015703 | 1.28228 | -4.2373 | ||
| 45 | 1.28039814 | 1.34256 | -4.855 | ||
| 50 | 1.34293127 | 1.39317 | -3.7408 | ||
| 55 | 1.42164737 | 1.50676 | -5.9868 | ||
| 60 | 1.52265858 | 1.65783 | -8.8775 | ||
| 65 | 1.65620238 | 1.7952 | -8.3923 | ||
| 70 | 1.84103351 | 2.01384 | -9.3865 | ||
| 75 | 2.11635939 | 2.38904 | -12.885 | ||
| 80 | 2.58376149 | 3.00631 | -16.354 | ||
| 85 | 3.64703164 | 4.68894 | -28.569 | ||
<2>를 보면
| 각도 | 주기(이론) | 주기(실제) | 오차(%) | ||
| 0 | 0.78913966 | 0.85953287 | -8.9202474 | ||
| 10 | 0.79520324 | 0.87387835 | -9.893710946 | ||
| 20 | 0.81406853 | 0.8975979 | -10.26072952 | ||
| 30 | 0.84798575 | 0.92264101 | -8.803834263 | ||
| 40 | 0.9016269 | 0.98482528 | -9.227584048 | ||
| 50 | 0.98428332 | 1.09654194 | -11.4051125 | ||
| 60 | 1.11601201 | 1.2368475 | -10.82743635 | ||
| 70 | 1.34936062 | 1.51402056 | -12.20281203 | ||
| 80 | 1.89373304 | 2.31851856 | -22.43111944 |
이와 같은 결과를 얻을 수 있었다.
4. 오차의 원인 분석
우선은 근사 과정에서의 오차를 생각할 수 있다.
측정 장비의 측정 오차(자로 잰 길이나 저울에 의한 길이)
진자를 진동시킬 때 생기는 마찰력과 공기저항을 들 수 있을 것이다.
5. 출처
연세대학교 교양물리 실험실
한양대학교 역학실험 매뉴얼
고려대학교 일반물리학 실험실
Classical Dynamics of Particles and Systems (marion),
'Classical Mechanics > Experiments - Lynx' 카테고리의 다른 글
| 역학실험 6- 진폭이 큰 진자의 주기 - 2 (0) | 2021.07.25 |
|---|---|
| 역학실험 6 - 진폭이 큰 진자의 주기 - 1 (0) | 2021.07.19 |
| 역학실험 4- 선운동량 보존/등가속도 운동 -(2) (0) | 2021.07.05 |
| 역학실험 4 - 선운동량 보존 & 등가속도 운동 -(1) (0) | 2021.06.28 |
| 역학실험 3 - 강제 조화 진동 (0) | 2021.06.25 |



