1. 실험 목적 & 소개
단순 조화 진동으로 근사할 수 없는, 큰 폭으로 진동하는 진자에서의 운동을 분석하는 것이 목적이다. 이번 주제는 두 번에 걸쳐서 진행하는데, 우선 주기와 진폭 사이의 관계에 대해서 분석하였다.
이를 위해서 실험 1에서는 다음의 다섯 가지를 분석하였다.
· θ가 충분히 작을 때
· t/t0그래프 그리고 확인하기
· θ가 0°~90°까지 10°간격으로 변할 때, t0에 대해서 얼마나 벗어나는지 이론적으로 예측하기
· 위의 오차가 1%가 되는 순간은 언제인가?
· 각도θ가 180°인 경우는 Unstable 하게 평형상태를 이루는 것이다. 이 때 주기는 무한대가 나온다. 그렇다면 θ가 0도인 것도 주기가 무한대라고 말할 수 있는가?
2. 기본 이론
진폭이 작은 물리 진자의 주기

강체가 질량 중심이 아닌 다른 고정점에서 진동하는 경우, 그 운동은 단진자에 가깝다. 실험 4에서 보았듯, T=2π sqrt(I/MgL_eff))로 나오며, 근사하면 T=2π sqrt(L/g)이다. 이는 상술하였듯이 진폭이 매우 작은 경우에나 성립하는 것이다.
진폭이 매우 작은 경우, θ≈sinθ 로 근사 가능하기 때문에 미분방정식이 linear하다고 가정한 결과인 것이다.
진폭이 매우 큰 경우
그러나 진폭이 매우 큰 경우부터는 θ≈sinθ 라고 근사할 수가 없다. 따라서 미분방정식 역시 nonlinear한 꼴을 그대로 사용하여서 풀어야 한다.

이 미분 방정식의 풀이를 위하여 타원 적분을 사용하여야 하며, 이렇게 해서 구한 진자의 주기는 다음과 같다.
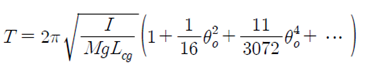
타원 적분의 개념을 이용한 주기 구하기

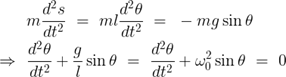
양변에 dθ/dt를 곱해서 정리하면 미방의 해를 비교적 쉽게 얻을 수 있다.
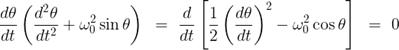
이를 시간에 대해 적분하면

이제 초기 조건을 마지막 식에 대입하면 진자의 위치별 각속도를 정확하게 얻는다.
진자는 θ=0,-θ_0,0,θ_0 을 순차적으로 거치며 주기 운동을 한다.
따라서

의 꼴이 등장한다. 이 식을 정리하면

이 나오며, 이를 제 1 종 완전 타원 적분(complete elliptic integral of the first kind)라고 한다.
이를 사용해서 진자의 주기에 대한 최종식을 얻는다.


보다시피 타원의 둘레 길이와는 무관한 식이지만, 피적분 함수의 역수를 취하면 타원의 둘레 길이를 표현하는 제2종 타원 적분이 나오기 때문에 타원 적분이라고 부른다
1) 실험 내용

1) θ0 가 19.2°일 때의 θ,θ',θ''의 주기를 구했다. θ가 충분히 작아, 모두 같은 주기를 보였다.

θ0 가 102°일 때의 θ,θ',θ''의 주기를 구했다. 모두 7.5초 정도의 주기를 보였다.
아래의 표에 정리되어 있다.
ω0=1.1rad/s
| θ0 | T(θ) s | T(θ') s | T(θ'') s |
| 19.2 | 6.1 | 6.1 | 6.1 |
| 102 | 7.5 | 7.5 | 7.5 |
| t/t_0 19.2 | 1.067946 | 그래프에서의 값 | 1.00 |
| t/t_0 102 | 1.313048 | 그래프에서의 값 | 1.24 |
자료로 주어진 t/t_0의 그래프와 우리가 잰 값 사이에서의 차이를 19.2도에서와 102도에서 각각 알아낸 것이다.
그래프 값을 이렇게 읽어서 ‘그래프에서의 값’을 얻어내었다.

각각의 경우에서 이론적으로 19.2° 일 때와102° 일 때의 주기를 비교하였다. 이를 위해서 1종 타원적분계산기로 k값을 이용하여 K와 주기를 계산하였다.
k=sinθ0 /2
을 사용한 것이다.

2) 1종 타원적분 계산기를 이용해서 주기와 초기 진폭에 대한 그래프를 그렸다.
10도부터 90도까지 10도 간격으로 계산한 것이다.

이와 같이 증가하는 모습을 볼 수 있다. K에 2π 를 곱하면 t/t0
를 구할 수 있다.

3) 이 때 t0 에 대해서 생기는 오차가 1%이하로 떨어질 때는 언제인지 알아보았다>
그래프를 읽은 결과, 단진자에서 예측한 주기와의 차이가 1%까지 난 것은 대략 35도부터 발생하였다.
4) θ0=180의 의미
180도일 때 진자는 Unstable 한 평형 상태를 이루게 된다. 따라서 주기도 무한대이다.

에 대입하였을 때

에서 무한대가 나오는 것이다.
그러면 θ0=0 일 때도 주기가 무한대라고 말할 수 있는가?
이 때는 K가 π/2이 나온다. 따라서 T=T0만 나오므로 주기가 무한대라고 말할 수 없다.
1. 오차의 원인
1) 정확하지 않은 데이터 읽기
주어진 데이터에서 각도를 읽을 때 정확한 눈금이 없어, 선을 긋되, 곡선 그래프에 비례 관계를 이용해서 데이터를 구해야 했다. 여기서 오차가 발생했을 것이다.
2) 주기를 잴 때도 마찬가지의 오류가 생겼다.
참고문헌
https://keisan.casio.com/exec/system/1180573451
Complete elliptic integral of the 1st kind K(k) Calculator
Calculates the complete elliptic integral of the first kind K(k).
keisan.casio.com
고려대학교 일반물리실험실
한양대학교 역학실험 매뉴얼
https://ghebook.blogspot.com/search?q=%ED%83%80%EC%9B%90%EC%A0%81%EB%B6%84
조금은 느리게 살자
물리학, 수학, 전자파, RF, 초고주파, 안테나, 통신 이론, 정보 이론
ghebook.blogspot.com
'Classical Mechanics > Experiments - Lynx' 카테고리의 다른 글
| 역학실험 7 (마지막) - 비틀림 진자 (0) | 2021.08.02 |
|---|---|
| 역학실험 6- 진폭이 큰 진자의 주기 - 2 (0) | 2021.07.25 |
| 역학실험 5 - 기울어진 진자의 운동 (0) | 2021.07.12 |
| 역학실험 4- 선운동량 보존/등가속도 운동 -(2) (0) | 2021.07.05 |
| 역학실험 4 - 선운동량 보존 & 등가속도 운동 -(1) (0) | 2021.06.28 |



