선운동량 보존에 대한 이론과 실험 설계입니다만 사정상 평균 속도에 대해 다루는 실험에 그쳤습니다.
1. 목적
선운동량 보존 법칙을 직접 실험을 통하여 확인한다.
2. 장비



에어트랙에 글라이더를 올려서 그 위에서 글라이더끼리의 충돌을 관찰하는 것이다.
글라이더에 추가 질량을 부착하여 질량을 조절한다. 그 외 글라이더의 앞 뒤에 붙은 고무밴드 범퍼 등의 질량도 항상 고려되어야 한다.
질량체는 항상 대칭으로 부착해야 한다.(양 측면에 동일한 수의 질량체를 부착해야 한다. 그렇지 않으면 글라이더가 제대로 작동하지 않는다.

고무밴드 범퍼


범퍼 블레이드


후크

도르래


에어트랙용 질량체 / 걸이 세트

3. 장비 조립


에어트랙 수평조절
에어트랙을 평평하고 안정된 테이블 위에 올려놓고, 에어트랙이 최대한 수평을 이룰 때까지 두발 받침대의 수평조절 나사를 돌려준다.
에어 서플라이 작동 조절
에어 서플라이는 에어트랙을 경미하게 가열시켜, 에어트랙이 팽창하게 된다. 트랙 아래에는 조절용 빔이 설치되어 있어, 에어트랙 작동 5분 후 또는 트랙이 따뜻해졌을 때, 트랙이 ±0.04mm 범위 내에서 일직선을 이루도록 한다.
4. 이론적 배경 - 선운동량 보존
1. 운동량의 정의 : p =mv
선운동량 보존 법칙 유도
고립된 질점계에서 물체에 작용하는 외력의 합이 0이면 운동량은 보존된다
F=dpdt=0
p=constant
질점 1이 느끼는 질점 2의 작용력
:
F12=dp1dt
질점 2가 느끼는 질점 1의 작용력
:
F21=dp2dt
이 때 두 힘은 서로 작용-반작용 관계이므로 크기가 같고 방향이 반대이다.
F12+F21=0
dp1dt+dp2dt=0
ddt(p1+p2)=0
p1+p2=p=constant (vector)
이렇게 해서 운동량 보존 법칙을 유도할 수 있다. 한편, 전체 운동량이 보존되므로 각 성분에 대해서도 운동량 보존은 성립한다.
p1i+p2i=p1f+p2f

충돌의 종류 – 탄성/비탄성/완전 비탄성
충돌의 종류에 따라서 보존되는 물리량이 다르다.
| 충돌 종류 물리량 |
탄성 | 비탄성 | 완전 비탄성 |
| 운동량 | O | O | O |
| 운동에너지 | O | X | X |
크게 탄성충돌/비탄성 충돌의 두 가지로 나누어 보았을 때 탄성 충돌에서는 운동량과 운동 에너지가 모두 보존되고, 비탄성 충돌에서는 운동량만 보존된다.
완전 비탄성 충돌이란, 충돌 뒤에 물체가 서로 붙어서 운동하는 경우를 말한다.

이 떄 에너지 손실량을 계산하여 보자. 초기 운동에너지와 나중 운동에너지의 차이를 구하면 되는 것이다.

지금까지 일차원일 때의 선운동량 보존 법칙을 다루었다. 2차원, 3차원에서는 각각의 축(x,y,z)에 대해서 1차원에서의 선운동량 보존 법칙을 그대로 적용하면 된다.
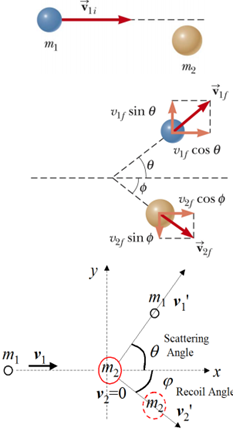
5. 실험
1) 완전 비탄성 충돌
두 글라이더가 충돌한 뒤 하나로 합쳐져 운동할 때 충돌 전후의 속도변화를 측정하는 것이다.

왁스튜브가 장착된 면이 서로 마주보도록 카트를 배치한다.
니들과 왁스튜브가 장착되지 않은 쪽에는 질량이 동일한 부속품(범퍼 블레이드, 후크 등)을 장착하여 카트가 평형을 이루도록 만든다.
2) 충돌 전 하나의 카트만 움직이는 경우
실험 1) 과 같은 종류의 충돌이나, 둘 중 하나는 정지한 상태일 때의 충돌이다. 실험 방법은 모두 1)과 같다.
2-A) 두 카트의 질량이 같을 때
예상 질문 : 충돌에서 운동량이 보존된다는 가정 하에, 충돌 후 카트의 속도를 예측해보자. 속도는 증가할 것인가, 감소할 것인가? v′ 대 v0의 비율은 얼마가 될 것인가?
예시 답안 : 전체 운동량은 p=mv_0로 일정한데, 질량은 두 배가 되었으므로 v'은 v_0의 절반이 될 것이다.
2-B) 두 카트의 질량이 다를 때
카트 2의 양 측면에 원형 질량체를 올려 카트의 질량을 변화시킨 다음, 실험 A의 과정을 반복한다.
3) 탄성 충돌 - 두 카트가 모두 움직이는 경우

카트 A와 B에 고무밴드 범퍼를 서로 수직이 되게 장착한 다음, 범퍼끼리 서로 마주보도록 카트를 배치한다. 범퍼가 장착되지 않은 쪽에는 질량이 동일한 부속품(범퍼 블레이드, 후크 등)을 장착하여 카트가 평형을 이루도록 만든다.
4) 충돌 전 하나의 카트만 움직이는 경우

1. 실험 3) 과 같은 종류의 충돌이나, 둘 중 하나는 정지한 상태일 때의 충돌이다. 실험 방법은 모두 3)과 같다.
3-A) 두 카트의 질량이 같을 때
예상 질문 : 카트 A를 정지해있는 카트 B쪽으로 밀면 어떤 일이 발생할지 예측해본다. 충돌 후 카트의 속도 와 의 상대값은 얼마가 될 것이라고 예측하는가?
예시 답안 : 운동량은 보존되고, 운동에너지도 보존된다. 따라서 두 카트의 상대 속도는 충돌 전후에 크기는 같고 방향은 반대일 것이다.
3-B) 두 카트의 질량이 서로 다를 때
카트 B의 양 측면에 원형 질량체를 올려 카트의 질량을 변화시킨 다음, 실험 A의 과정을 반복한다.
이렇게 실험 A),B)로 나누어서 실험을 진행할 것이다.
측정값을 이용하여 운동량과 운동에너지를 계산한다. 충돌 전후 총 운동량 과 사이의 백분율
변화를 계산하여 운동량이 보존되었는지 확인한다. 마찬가지로 운동에너지가 보존되었는지 확인한다.
6. 출처
그림 자료들 및 완전 비탄성 충돌에서의 에너지 손실 http://contents.kocw.or.kr/KOCW/document/2014/gacheon/ohchangheon/9.pdf
실험 자료들 : 한양대학교 역학실험 매뉴얼, 연세대학교 역학실험 매뉴얼
'Classical Mechanics > Experiments - Lynx' 카테고리의 다른 글
| 역학실험 5 - 기울어진 진자의 운동 (0) | 2021.07.12 |
|---|---|
| 역학실험 4- 선운동량 보존/등가속도 운동 -(2) (0) | 2021.07.05 |
| 역학실험 3 - 강제 조화 진동 (0) | 2021.06.25 |
| 역학실험 2 - Chaos (0) | 2021.06.25 |
| 역학실험 1 - 자이로스코프 배경이론 (2) | 2021.04.04 |



