1. 실험 목적 및 소개
고전 역학적 관점에서 나타나는 Chaos 현상을 간단히 구현하여 본다.
Chaos 현상의 해석을 위하여 Potential Well, Phase Diagram을 활용한다.
2. 기본 이론
카오스란?
± 19세기 초 프랑스의 라플라스의 결정론적 세계관(Stephen T. Thornton, Jerry B. Marion, 2004)
± 우주의 모든 입자들의 위치와 속도를 알고 있으면 어떤 시간에 대해서도 미래를 알 수 있다고 주장
± 카오스(chaos, 혼돈)은 불규칙하고 예측불가능하다는 점에서 동전을 던지는 것과 같은 무작위 현상과 같다고 오해
± 카오스 현상은 계가 한 상태에서 다음 상태로 발전할 때 ‘물리법칙’이라는 규칙이 존재
± 결정론적 카오스는 항상 3개 이상의 변수로 이루어진 비선형계와 관련되어 있다(김영태, 1998)
± 비선형계는 운동방정식을 이루는 변수가 선형적이지 않은 것, 완전해를 구할 수 없다
± 위상공간, 푸앵카레 단면과 같은 그래프의 모양 분석을 통해 물체의 운동을 분석
(Stephen T. Thornton, Jerry B. Marion, 2004)
Attractor (끌개)
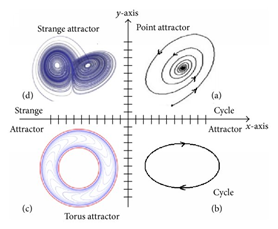
± 초기 항의 효과가 사라진 긴시간 이후 위상공간에서의 점들의 집합
± 끌개(attractor)의 모양에 따라 주기 운동과 카오스 운동이 구별
± 어느 특정 영역에서 주기운동으로 빠짐
± 초기 상태와 무관
비선형 진동자의 예시




Simple Harmonic Oscillator
± mx+kx=0
± Damped Oscillation : mx+bx+kx+cf(t)=0
⇔(md2dt2+bdydx+k)x(t)=-cf(t)
± C = 0 인 경우, (Homogeneous) 단순한 진동자 문제. 해의 선형성 보장
± L(x1)+ L(x2)= L(x1+x2)
± F(t)가 Analytic 하지 않은 문제가 생길 경우에 Nonlinear
± 해를 구하기 어려움
± Homogeneous 한 경우 Periodic 보장 가능
± Nonhomogeneous한 경우 non-periodic
± Analytic Solution이 없음
± Shooting Method, Runge Kutta Method 등의 수치해로만 풀이 가능
Potential Well

± S.H.O
± mx+kx=0
± F=mx=-kx=-∂V∂x
± Damped Oscillator
± mx+bx+kx = 0
± →H=1/2mx2+1/2kx2+∫bx^2dt
(Nonfriction 인 경우 b=0
Friction 에 관한 Solution x=exp(-Bt)sinωt꼴
± 마찰이 작용하는 경우, 진폭이 계속 감소하는 운동
± U=1/2kx^2-1/2mω^2A02exp(-Bt)
Phase Space
± Chaos 현상 연구를 위해 Hamiltonian은 필수
± Hamiltonian은 본질적으로 운동량과 위치의 함수
± 위치와 운동량으로 이루어진 공간이 Phase Space
± Harmonic Oscillator
± Underdamped Oscillator
± Critically damped Oscillator
± Underdamped Oscillator




Poincare Section
± 위상공간 속에서 이들의 평행면으로 된 위상 궤도의 구역에 찍은 점의 궤적
± 위상공간 도표를 순간카메라로 찍은 것과 유사함
± x=θ,z=ωt',y=θ
± SHO의 경우 투사된 모든 점은 같다.
± Z가 2π
까지 가면 다시 (x.y)로 돌아오니까

3. 실험 결과
실험 준비
± 알루미늄 원판에 두 개의 스프링이 연결된 구조
± 원판에 달린 점질량이 Nonlinear함을 만들어냄
± Sinusoidal 한 driving force
± Predictable Motion에서 Chaotic Motion으로 전환
실험 장비
Driver Photogate Tying the String Complete Magnetic Drag
실험1) Chaotic Motion
Figure 1: < Phase Diagram > |
Potential Well 이 두 개 관찰되는 중
Poincare point(굵은 점) 가 여러 곳에 찍힌다.
Figure 2: < Potential Well> |
Potential Well 이 두 개 나타남을 관찰할 수 있었다.
갑자기 크게 에너지가 변한 곳은 손가락으로 쳐서 비선형적인 효과를 극대화 하려고 해 본 부분이다.
2) Non – Chaotic Motion
Figure 3: Phase Space of Non chaotic motion |
Non Chaotic Motion에서의 Phase space를 그려 보았다. Chaotic 일 때와 달리 하나의 닫힌 곡선(타원에 가까운) 을 그리고 있었다.
주기적인 운동이기 때문에 Poincare point도 (밝은 점) 계속 같은 위치에 찍혔다.
Magnetic drag를 거의 주지 않음
Figure 4: Potential Well of Non Chaotic motion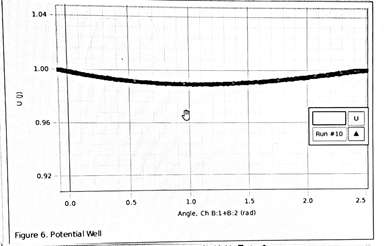 |
Non Chaotic Motion에서의 Potential Well.
S.H.O에서처럼 이차함수 모양을 그리고 있다.
Figure 5: Damping |
Damping 의 효과로 Potential Well 이 점점 채워지고 있다.
4. 결론 및 관찰 결과
두 개의 Potential well(두 개의 용수철이 갖고 있는 탄성 에너지에 의한) 을 넘나드는 모습을 관찰하였으나, 나중에는 한쪽 Potential Well에만 빠지는 모습을 볼 수 있었다.
이를 통해서 우리 실험에서는 배경 이론에서 언급한 Attractor의 모양이 원형으로 나타나고 있다는 결론을 내렸다.
또한, Attractor 의 모양은 초기 조건과 무관하게 나타나는 것도 관찰할 수 있었다. 한쪽 퍼텐셜에 빠진 것을 보고 손가락으로 점질량을 건드려서 반대편 Potential Well에 빠지게도 해 보았으나 이내 다시 나와서 다른 Potential Well에 빠지는 것을 본 것이다. (이후 Poincare point 도 거의 한쪽에만 찍힘)
왼쪽에 Phase 곡선이 타원형으로 점점 굵게 나타나고 있음을 볼 수 있다.

Reference
± Classical Dynamics of Particles and systems 5th edition (Stephen T.Thornton, Jerry B.Marion)
± Fowels,Cassiday Analytical Mechanics
± https://web.archive.org/web/20051227123602/http://physics.mercer.edu/pendulum/
± https://en.wikipedia.org/wiki/Harmonic_oscillator
± 카오스 진자의 비주기적 운동 분석과 커플 진동에서 표준 진동수와 진자의 관성모멘트 비의 영향 연구
(Analysis of Non-periodic Motion for the Chaos Pendulum & the Effect of Normal Frequency and Ratio of Moment of Inertia for the Coupled motion, 서울대학교 과학교육과 박수정)
https://s-space.snu.ac.kr/bitstream/10371/128095/1/000000141390.pdf
± Intermediate Dynamics (Patric Hamill, 강지훈, 송승기, 양우철, 이영재 역)
± https://www.slowpokeproductions.com/
± https://gfycat.com/animatedeverlastingbagworm-engineering-mathematica-simulation
± http://phylab.yonsei.ac.kr/board.php?board=sensor&command=body&no=6
'Classical Mechanics > Experiments - Lynx' 카테고리의 다른 글
| 역학실험 4- 선운동량 보존/등가속도 운동 -(2) (0) | 2021.07.05 |
|---|---|
| 역학실험 4 - 선운동량 보존 & 등가속도 운동 -(1) (0) | 2021.06.28 |
| 역학실험 3 - 강제 조화 진동 (0) | 2021.06.25 |
| 역학실험 1 - 자이로스코프 배경이론 (2) | 2021.04.04 |
| 역학실험 1 - 자이로스코프 실험결과 (0) | 2021.04.04 |



