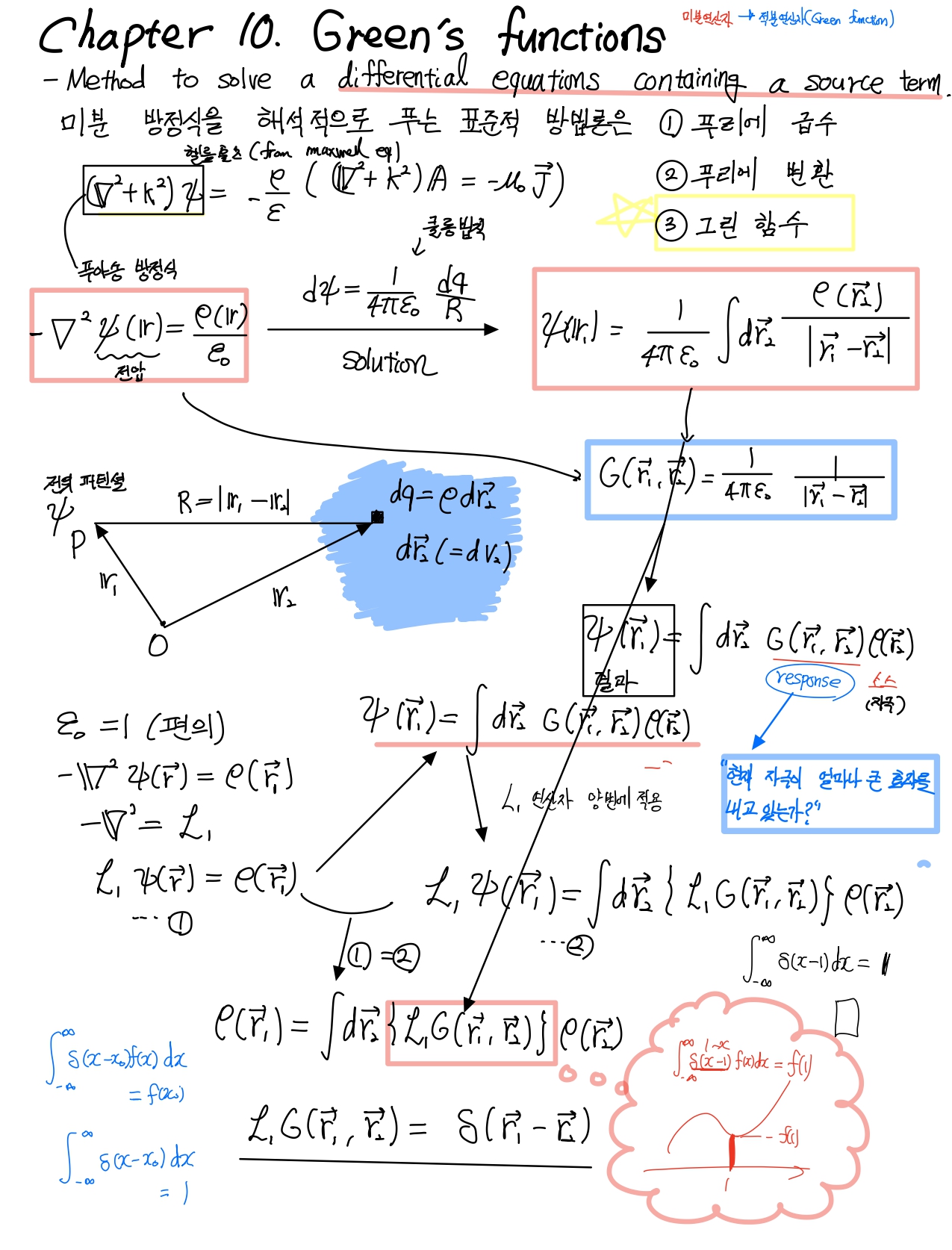
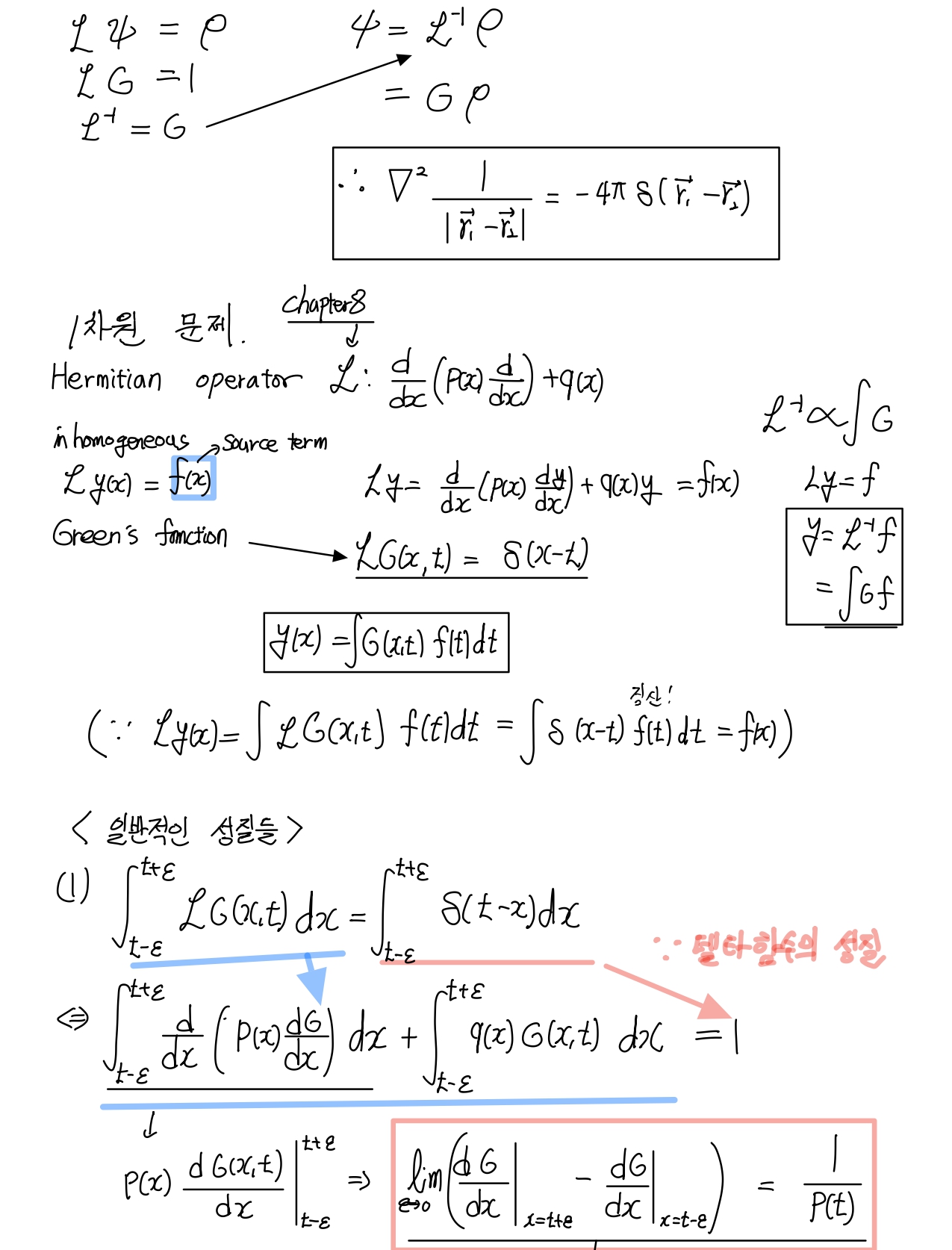


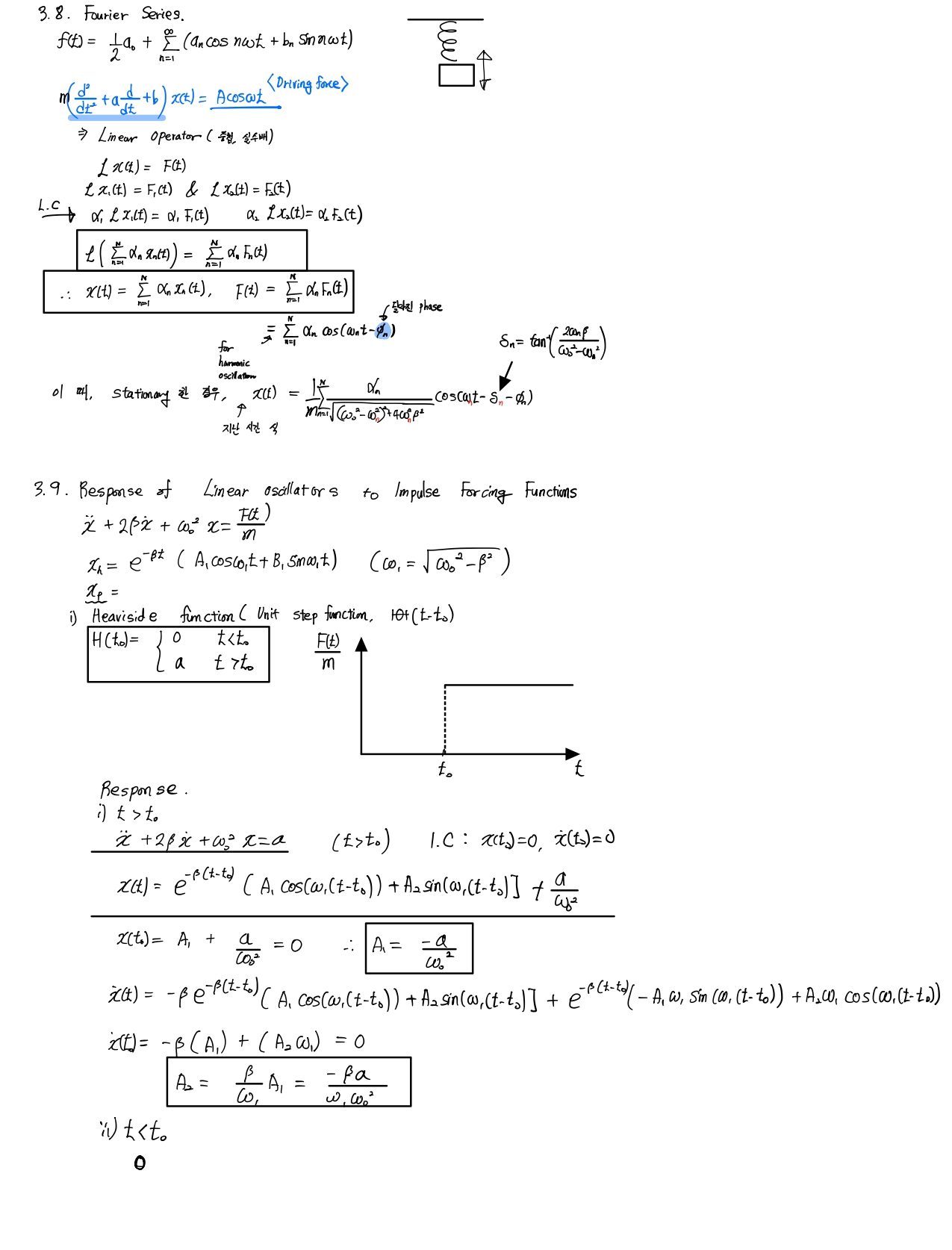


Q. \[g_{nm}\] 은 무엇인가요?
A. 좋은 질문입니다. 이에 대한 답을 3번째 슬라이드에서 expansion of dirac delta function에 넣어 두었습니다.
Q2. Green's function은 solution이 central force에 의한 것일 때만 사용하나요?
A. 이거 저도 잘 모르겠어서 한번 찾아봤는데

3D에서는 그런 항이 포함되기는 하지만 모든 경우에 다 그렇지는 않은 듯 합니다. 오늘 처음으로 예시를 들었던 Poisson Equation의 해가 저 (3,1) 성분에 있는 건데 저걸 먼저 다루다 보니, 그리고 Sinusoidal function이 driving force 인 경우를 다루다 보니 저도 착각한 것 같습니다.
Reference: Classical Dynamics of Particles and Systems, Mathematical Methods for Physicists, 7th ed
https://slideplayer.com/slide/7362188/
講者: 許永昌 老師 1. Contents Green’s function Symmetry of Green’s Function Form of Green’s Functions Expansions:
Green’s Function ( 請預讀 P592~P594) L : linear Operator Green’s Function obeys: [z L ] G(r,r’)= (r r’) where z is a constant. Or [zI L]G=I. G is the inverse Operator of [z L]. Therefore, if [z L (r 1 )
slideplayer.com
Green's function animation - Green's function - Wikipedia
Green's function - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Impulse response of an inhomogeneous linear differential operator This article is about the classical approach to Green's functions. For a modern discussion, see fundamental solution.
en.wikipedia.org
추가로, 그린 함수에 대한 직관적인 설명을 보여 주고 있는 gif 이미지를 첨부합니다.
그린 함수에 대해서만 전문적으로 300페이지를 할애하는군요.
'Classical Mechanics > Team Project -' 카테고리의 다른 글
| 4-2.Elliptic integral and plane pendulum (0) | 2021.07.24 |
|---|---|
| 4-1.Nonlinear oscillations and Chaos (1) | 2021.07.24 |
| 2.Newton Mechanic (1) | 2021.07.17 |
| 3. Oscillation - 1 (0) | 2021.07.14 |
| 1. Levi-civita Symbol and Kronecker-delta (2) | 2021.07.03 |



