Levi civita 를 정의하기에 앞서서 행렬식(Determinant)에 대한 계산법부터 간단히 짚고 넘어갑니다.
우선은 2 by 2 행렬의 행렬식, 3 by 3 행렬식의 계산법은

이와 같습니다. 2 by 2 의 경우는 ad-bc이고, 3 by 3 행렬식은 맨 윗줄의 a와, a와 행번호 열번호가 하나라도 같은 b, c ,d,g 를 지우고 남은 소행렬 \begin{pmatrix} e & f \\ h & i \end{pmatrix}
의 행렬식을 구하여 곱해 준다. 나머지 b, c 에 대해서도 소행렬식과 coefficient expansion을 이용해서 계산한다.
그냥 쉽게는 저 그림처럼 1열, 2열을 뒤에 붙인 뒤, 신발끈대로 곱해서 더하고 빼면 된다.
이제 본격적으로 levi-civita 기호를 설명한다.이를 위해서 우선 위의 3 by 3 행렬을 성분별로 표시하였다.
이 때 성분들은 시그마 합 기호를 이용해서 아래와 두 번째 줄과 같이 표현 할 수 있다.

그러면 Levi civita는 어떤 값을 가지길래 저렇게 정리할 수 있는 것일까?

이처럼 1 2 3을 odd permutation 하면 -1, even permutation 하면 1이 나온다. 이는 앞서 언급한 행렬식 때문이다.
column vector $$ \overrightarrow{e_1}\ $$, $$ \overrightarrow{e_2}\ $$, $$ \overrightarrow{e_3}\ $$를 조합해서 만든 기본 행렬(Elementary Matrix)들의 행렬식을 구해 보면 저 성질을 잘 이해할 수 있다.

이를 적용하여서 여러 가지 문제들을 풀어 보자.
먼저 벡터의 외적이다.
벡터의 외적은 두 벡터 $$ \overrightarrow{A}\ $$, $$ \overrightarrow{B}\ $$ 가 포함된 평면에 대해서 수직으로 생긴 벡터 $$ \overrightarrow{C}\ $$로 정의되며, 이 $$ \overrightarrow{C}\ $$ 의 크기는 $$ ABsin(\theta )\ $$ 이다.
이를 Levi civita 기호를 이용해서 표현하면

levi civita의 성질상 같은 번호가 반복되면 0이 되기 때문에 위와 같이 표현할 수 있는 것이다.
벡터 외적과 내적을 동시에 사용하는 예제도 있다.

내적은 성분끼리의 곱이므로 위와 같은 연산이 나온다.
또한, $$ \varepsilon_{ijk}\ $$ = $$ \varepsilon_{jki}\ $$ = $$ \varepsilon_{kij}\ $$ 이므로 순서를 바꿔도 같은 값이 나온다.

중간에 빨간색 글씨가 시작되는 부분부터 Kronecker-delta가 나오기 시작한다. 이 Kronecker-delta가 어떻게 나왔는지에 대해서 설명한 것이 빨간 네모박스 아래부터이다.
그러나 이런 설명은 조금 어렵고 직관적이지 못하여, 다음의 설명을 추가한다.
논문 Boosting Vector Calculus with the Graphical Notation 에 의하면 이렇게 쉬운 그림으로 설명할 수 있다.

(Joon-Hwi Kim∗ Department of Physics and Astronomy, Seoul National University, Seoul, South Korea Maverick S. H. Oh† and Keun-Young Kim‡ Department of Physics and Photon Science, Gwangju Institute of Science and Technology, Gwangju, South Korea (Dated: November 5, 2019)
이 notation 의 ecosystem 에 대해서 알아들을 수 있도록 다음의 논문을 첨부한다.
(PDF) Boosting Vector Calculus with the Graphical Notation (researchgate.net)
(PDF) Boosting Vector Calculus with the Graphical Notation
PDF | Learning vector calculus techniques is one of the major missions to be accomplished by physics undergraduates. However, beginners report various... | Find, read and cite all the research you need on ResearchGate
www.researchgate.net
무료로 다운받을 수 있는 논문이다.
다음으로 백캡 공식에 대한 증명이다. (이 백캡 공식은 \mathbf{Del operator} \Del 에 적용할 때는 주의하여야 한다.)

이를 del

Kronecker Delta란 i=j일 때 1이고, \{i!=j} 일 때 0이 되는 기호이다. 기본적으로 단위 행렬과 (Identity Matrix)이다.
이 성질을 이용하면 a) 번 문제가 identity matrix의 Trace 임을 물어본다는 사실을 쉽게 알 수 있다.
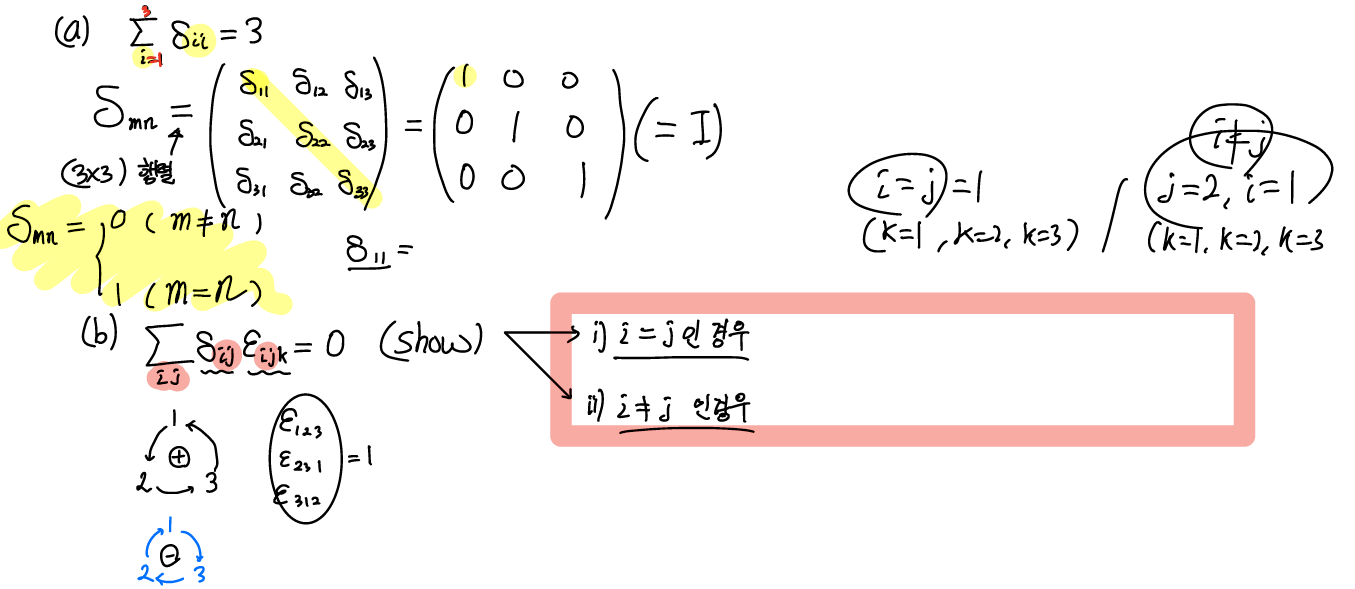
또한, 기본적으로 (단위) '행렬'이기 때문에 Ex4) 에서 크로네커 델타의 곱을 단순히 만들 수 있다.

Ex5는 우리가 아는 공식을 이용해서 푼 것이다.



levi-civita와 Kronecker delta 사이의 관계식을 유도한 것이다.
행렬식과 Transpose 한 행렬식은 서로 같다는 사실도 이용하였다.
levi-civita는 쉽게 적응하기 힘든 notation이다.
많은 연습만이 답일 것이다.
이것으로 첫 주의 스터디 정리 결과를 마친다.
Reference :
(PDF) Boosting Vector Calculus with the Graphical Notation (researchgate.net)
(PDF) Boosting Vector Calculus with the Graphical Notation
PDF | Learning vector calculus techniques is one of the major missions to be accomplished by physics undergraduates. However, beginners report various... | Find, read and cite all the research you need on ResearchGate
www.researchgate.net
Online LaTeX Equation Editor - create, integrate and download (codecogs.com)
Online LaTeX Equation Editor - create, integrate and download
Type your equation in this box
www.codecogs.com
Classical Dynamics of Particles and systems (Marion, Thornton, 5th ed)
'Classical Mechanics > Team Project -' 카테고리의 다른 글
| 4-2.Elliptic integral and plane pendulum (0) | 2021.07.24 |
|---|---|
| 4-1.Nonlinear oscillations and Chaos (1) | 2021.07.24 |
| 3. Oscillation 2 - Impulse and Green's function (0) | 2021.07.19 |
| 2.Newton Mechanic (1) | 2021.07.17 |
| 3. Oscillation - 1 (0) | 2021.07.14 |



