<script type="text/x-mathjax-config">
MathJax.Hub.Config({
tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]}
});
</script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/latest.js?config=TeX-MML-AM_CHTML"></script>
여기서는 매질의 광학적 성질에 대해서 간단히 논하려고 합니다.
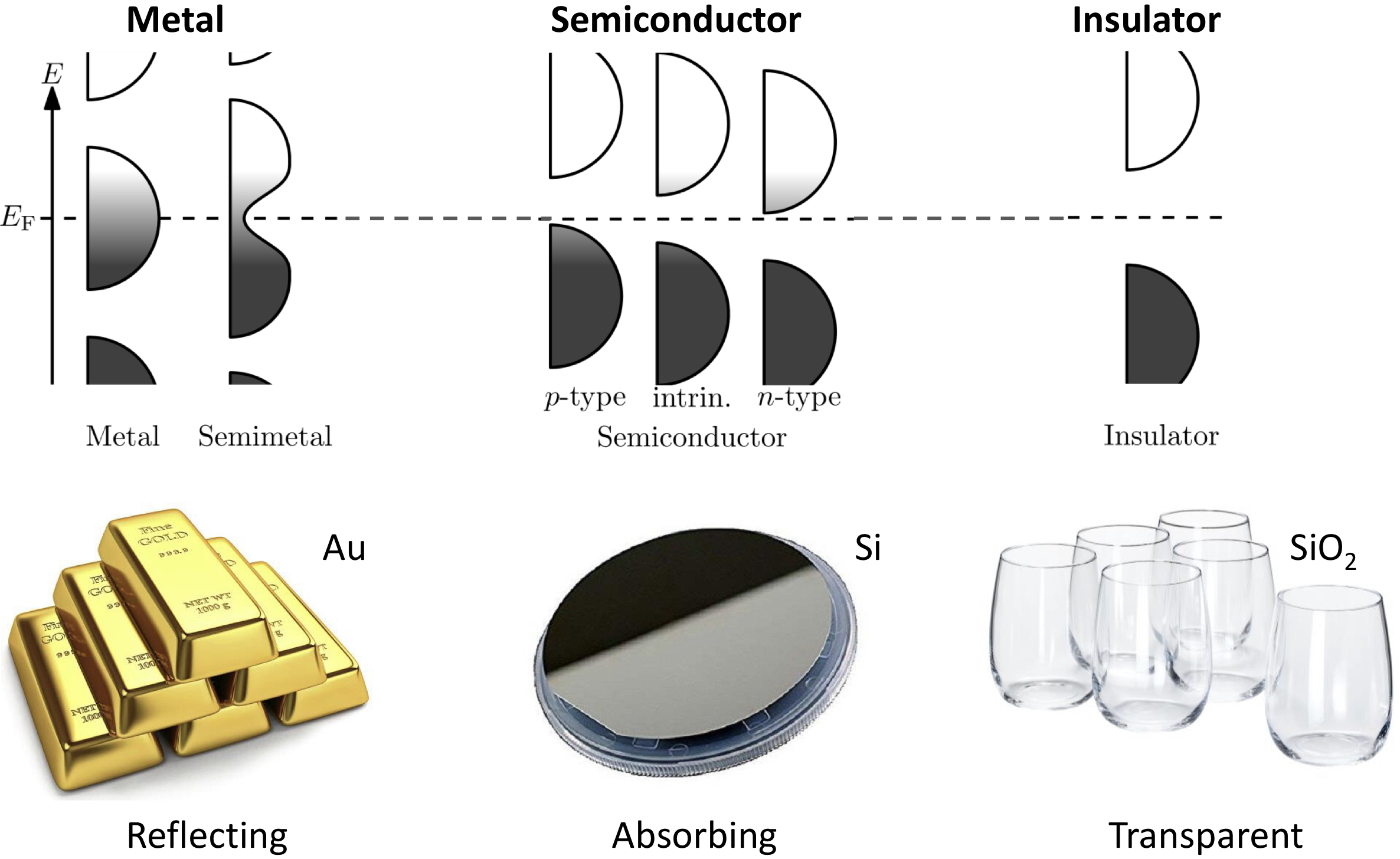
우선 이러한 분류의 모티프는 도체(금속)과 반도체, 그리고 부도체입니다.
금속의 경우는 다음과 같이 Conduction band 와 Valance Band 가 서로 붙어 있어, 전자가 자유롭게 이동하여 자유 전자가 됩니다. 이 자유 전자 때문에 금속의 많은 성질이 발생합니다. 광학적으로는 자유 전자가 빛을 반사하여 금속은 불투명하게 됩니다.
반도체는 빛을 흡수하는 성질이 있습니다.
부도체는 전자기파에 대해 투명합니다.
유전율 (Permittivity)
속박전하에 전기장을 가한 상황을 보면 다음과 같습니다.
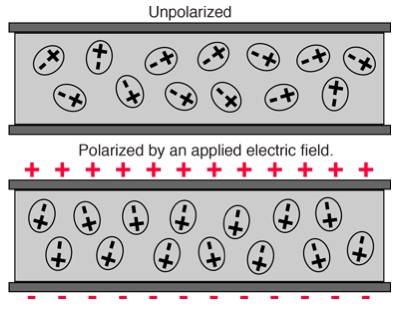
이 속박전하들이 전기장에 대해 얼마나 응답(Response)하는지에 대한 척도를 알아야 할 것입니다. 이 척도를 permittivity 와 electric susceptibility를 이용해서 Polarization이라는 물리량으로 나타냅니다.
polarization 식은 다음과 같습니다.
전도도(Conductivity)
옴의 법칙은 다음과 같습니다. J=σE. σ가 바로 전도도 입니다. 이 역시 자유 전하가 전기장에 대해 얼마나 응답(Response)하는지를 나타내는 척도입니다.
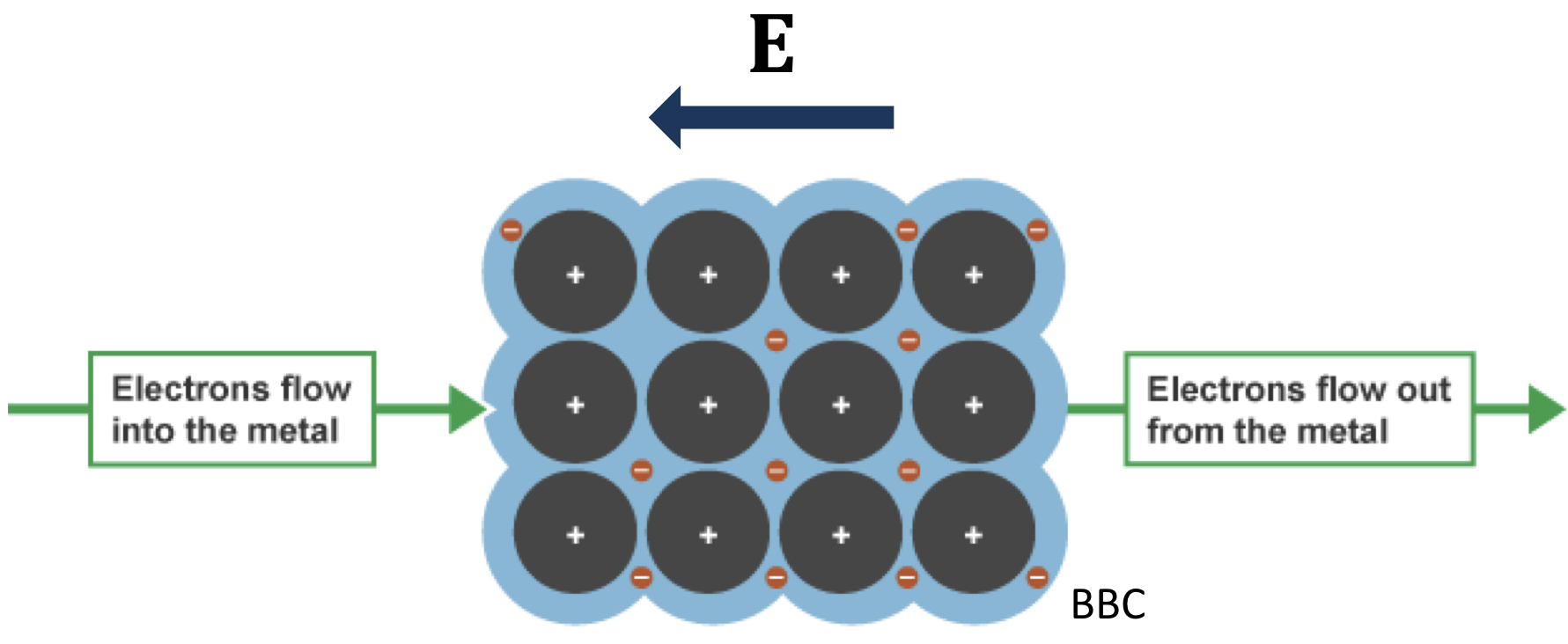
이제 유전율과 전도도를 서로 비교해 보도록 하겠습니다.
P=-ne<x>
J=-ne<\xdot>
<x> : 격자 이온에서 전자의 변위
이 때 전류 J를 t에 대한 식, ω에 대한 식으로 나타낼 수 있습니다.
J(t) = dP(t)/dt
J(ω) = -iωP(ω)
ε(ω)=1+iσ(ω)/(ε_0ω)
시간과 공간의 비국소성(Non-locality)
우선 비국소성에 대해 간단히 설명하겠습니다.
물리학에서 작용이란 멀리 떨어진 물체에 다른 물체에 의해 건드려졌다는 것을 의미합니다. 이렇게 공간상으로 멀리 떨어져 있는 경우의 상호작용을 비국소적인 상호작용이라고 합니다. (Non-locality)
예를 들어 중력에 의한 상호작용은 ‘즉시’ 일어나지 않습니다. 태양이 갑자기 사라진다면 우리는 그 변화를 8분 20초 뒤에(중력파의 속도는 빛의 속도와 같다고 생각되므로) 알아차리게 될 것입니다.
이런 관점에서 보면 위에서 쓴 Polarization와 J(current)식은 엄밀히 말하면 잘못되었습니다. 전기장의 작용에 의해 ‘즉시’ 반응하는 것으로 여겨서, 응답시간을 고려하지 않았기 때문입니다.
그래서 정확히는
P(r,t)= ε_0χE(r,t)
J(r,t)= σE(r,t)
이 아닙니다.
σ와 ε_0이 ‘응답’에 대한 척도임을 고려하여서 빛이 전자기파와 상호작용을 하는 과정에서 non-locality를 고려하여 수식을 작성하여야 합니다.
P(r,t)= ε_0χE(r,t)= ε_0integral(dt’dr’ χ(r-r’,t-t’)E(r’,t’))
J(r,t)= σE(r,t)=integral(dt’dr’σ(r-r’,t-t’)E(r’,t’))
'Photonics' 카테고리의 다른 글
| 4월 2일 Photonics 스터디 (0) | 2023.04.03 |
|---|---|
| Photonic crystal 이란? (2) (0) | 2023.02.25 |
| Photonic crystal 이란? (1) | 2023.02.25 |


