제가 맡은 부분에서는 앞단원의 결과를 그대로 가져다 쓰는 경우가 많습니다.
처음부터 그런게 나오는데, orthonormal 한 성질을 이용해서 Kronecker-delta 로 표현한 식은 사실 12.5절(Orthogonality of the Eigenvectors(Optional))에 나오는 내용입니다.
Characteristic Anguler velocity 에 대한 내용도 이 절에서 참고해 가져옵니다.


지금 여기서 궁금한건 12.4문제에서 Tensor {M} 이 왜 \[\begin{pmatrix} m & 0\\ 0& m \end{pmatrix}\] 이 아닌지입니다.
\[\begin{pmatrix} mb^2 & 0\\ 0& mb^2 \end{pmatrix}\] 라고 썼는데, 결과를 놓고 보면 왜 그렇게 놔야 하는지 알겠습니다만 문제를 푸는 과정에서는 왜 그렇게 했는지를 잘 모르겠습니다.
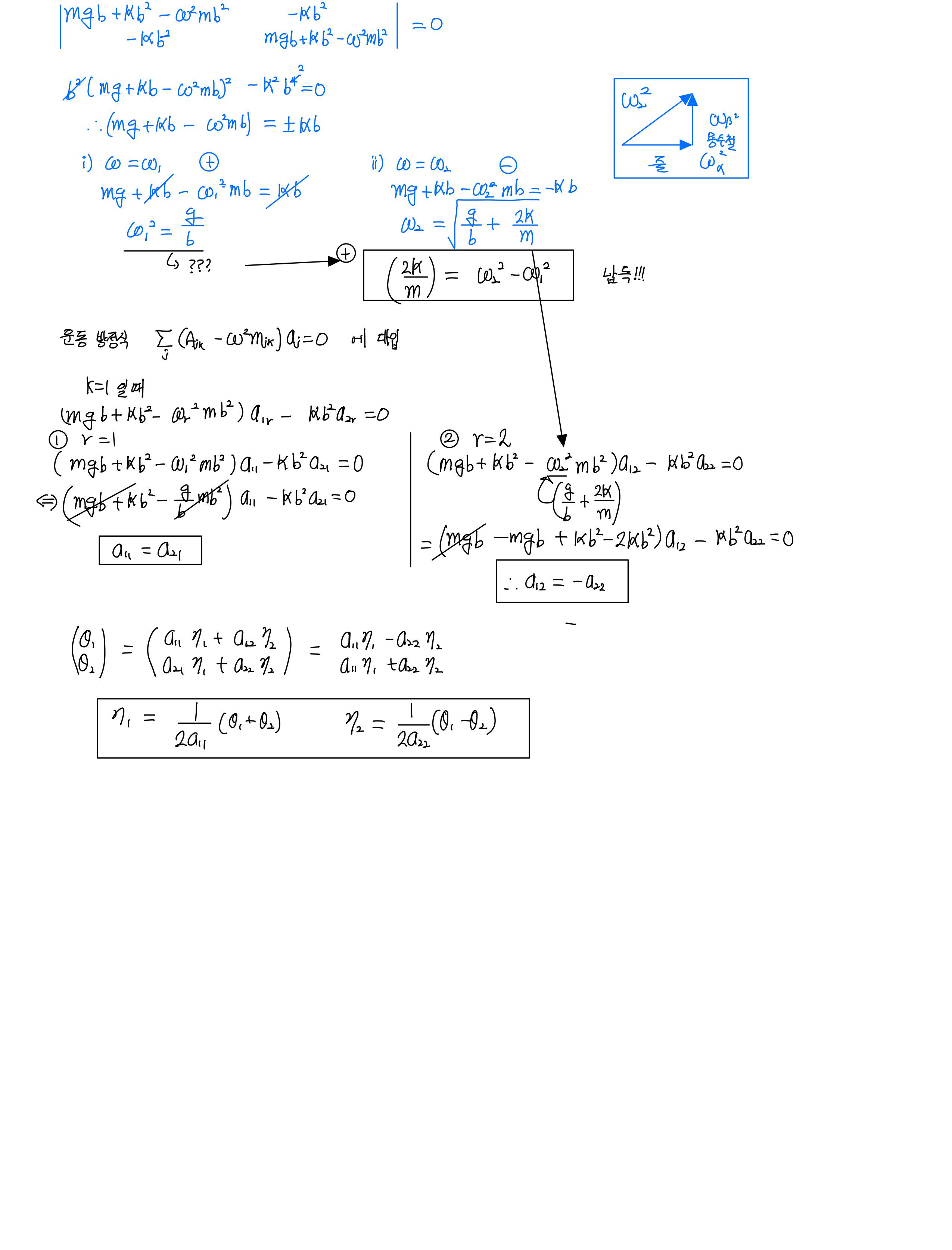
\[\omega ^2\]이 두 개 나오는데 둘 중 하나는 용수철에 의해 영향을 받고 하나는 용수철에 의한 영향을 받지 않는 상황으로 나왔습니다.
그리고 그 모양이 마치 \[\omega_1 ^2\] + \[\omega+2 ^2\]을 한 것과 같이 나와서 신기했습니다.
이걸 어떻게 해석할까 하다가 다른 팀원이 오히려 용수철에 의한 angular velocity 항을 가지고 표현되었다고 보아도 괜찮지 않을까 하는 관점을 내었습니다.
일단은 이렇게 생각하고 문제 풀이를 마쳤습니다.
Reference: Classical Dynamics of Particles and Systems(Marion) 5th ed.
'Classical Mechanics > Team Project -' 카테고리의 다른 글
| Pseudo vector 정리(feat 시립대 노재동 교수님) (0) | 2023.03.24 |
|---|---|
| 12.5 Orthogonality of Eigenvectors (0) | 2021.09.07 |
| 11단원. 문제풀이 (0) | 2021.08.28 |
| 12.9, 13.1.The loaded string and continuos string as a limiting case (0) | 2021.08.28 |
| 11.10 Force-Free Motion of a Symmetric Top (0) | 2021.08.21 |



